Fork me on GitHub

KMP/Trie树/Aho-Corasick Automaton 学习笔记

发表于 | 分类于
字数统计: 2,671字 | 阅读时长 ≈ 14分钟

继续填坑.
本来想把这三个玩意分开来写的,后来发现其实阿次自动姬就可以描述这几个的原理了.
那就写一起了.

KMP

全称叫做 (Knuth-Morris-Pratt).是能够在线性时间内完成字符串匹配的算法.

原理

KMP算法不同于一般的暴力匹配算法的地方在于,KMP算法充分利用了每次匹配后的失配信息,不会每一次都从第一个位置匹配,因此我们先介绍一个玩意叫做适配数组fail[i].

对于fail[i]数组的定义:

模式串中前i个字符作为目标串的最大前后缀对称长度.

这什么定义啊看得我头大.

我们以实际栗子来说明.

假设现在又这样的一个模式串shryshrkrin

根据定义我们推出的fail数组为00001230000

为什么这么定义fail数组呢?在我们匹配字符串的时候，如果之前的匹配失败了，我们直接用fail数组得到下一个合法的前缀即可.而且又可以证明,fail数组和匹配的串没有任何的关系,换言之,得到了fail数组,就是得到了失配信息.与下一个可能合法的字符串的位置.

好我们是不是只要能求出fail数组就可以收工了？

fail的递推方式如下.

  1. 如果 fail[i - 1] 不为 0，且第 i 个字符与第 fail[i - 1] +　１ 个字符相同，则 fail[i] 即为 fail[i - 1] + 1；
  2. 如果 fail[i - 1] 为 0，且第 i 个字符与首个字符相同，则 fail[i] = 1，否则 fail[i] = 0；
  3. 如果 fail[i - 1] 不为 0，且第 i 个字符与第 fail[i - 1] +　１ 个字符不同，则继续对比第 i 个字符与 fail[fail[i - 1]] + 1 个字符，一直向前找直到匹配或者找到了 0。

板子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

int kmp(char *a, char *b) //find b in a
{
	static int fail[MAXN];
	int na = strlen(a+1),nb = strlen(b+1);
	fail[1] = 0;
	for (int i = 2; i <= nb; i++)
	{
		int j = fail[i-1];
		while(j != 0 && b[j+1] != b[i]) j = fail[j];
		if (b[j+1] == b[i]) fail[i] = j+1;
		else fail[i] = 0;	
	}	
	int res = 0; 
	for (int i = 1,j = 0; i <= na; i++)
	{
		while(j != 0 && b[j+1] != a[i]) j = fail[j];
		if (a[i] == b[j+1]) j++;
		if (j == nb)
		{
			res ++;
			j = fail[j];
           // j = 0;
           //如果每个字符只能使用一次,这里的j应该为0
		} 
	}
	return res;
}

然后是板子题.

POJ-3461

板子题,求第一个串在第二个中的出现次数.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//#include<bits/stdc++.h>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAXN = 1e6+10;
char s1[MAXN],s2[MAXN];

int kmp(char *a,char *b)
{
	static int fail[MAXN];
	int na = strlen(a+1), nb = strlen(b+1);
	fail[1] = 0;
	for (int i = 2; i <= nb; i++)
	{
		int j = fail[i-1];
		while(j != 0 && b[j+1] != b[i]) j = fail[j];
		if (b[i] == b[j+1]) fail[i] = j+1;
		else fail[i] = 0;
	}
	int res = 0;
	for (int i = 1,j = 0; i <= na; i++)
	{
		while(j != 0 && b[j+1] != a[i]) j = fail[j];
		if (a[i] == b[j+1]) j ++;
		if (j == nb)
		{
			res ++ ;
			j = fail[j];
		}
	}
	return res;
}

int main(int argc, char *argv[])
{
	int T;
	scanf("%d",&T);
	while(T--)
	{          
		scanf("%s%s",s1+1,s2+1);
		printf("%d\n",kmp(s2,s1));	
	}
	return 0;
}

LUOGU-3375

还是板子题,求询问串的所有出现位置与next数组.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAXN = 1e6+10;
char s1[MAXN],s2[MAXN];
vector <int> v;
vector <int>::iterator it;
void kmp(char *a,char *b)
{
	static int fail[MAXN];
	int na = strlen(a+1), nb = strlen(b+1);
	fail[1] = 0;
	for (int i = 2; i <= nb; i++)
	{
		int j = fail[i-1];
		while(j != 0 && b[j+1] != b[i]) j = fail[j];
		if (b[i] == b[j+1]) fail[i] = j+1;
		else fail[i] = 0;
	}
	int res = 0;
	for (int i = 1,j = 0; i <= na; i++)
	{
		while(j != 0 && b[j+1] != a[i]) j = fail[j];
		if (a[i] == b[j+1]) j ++;
		if (j == nb)
		{
			v.push_back(i-j+1);//这个莫名其妙地自己蒙出来了.
			j = fail[j];
		}
	}
	for (it = v.begin(); it != v.end(); it++)
		cout << *it << endl;
	for (int i = 1; i <= nb; i++) cout << fail[i] << " ";
}

int main(int argc, char *argv[])
{
	v.clear();
	scanf("%s%s",s1+1,s2+1);
	kmp(s1,s2);	
	return 0;
}

那么再来一道.

算了看习题整理吧。

Trie树(字典树)

其实是个很斯波的东西.

很好写也很好懂.

HDU-1251

求询问串为模式串前缀的个数.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#pragma GCC optmize("0fuck")
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6+10;
char s[11];
struct Trie{
	int tot,trie[maxn][26],sum[maxn];
	void settledown(void){tot=0;memset(sum,0,sizeof(sum));}
	void insert(char *s,int rt)
	{
		int l = strlen(s);
		for (int i = 0; i < l; i++)
		{
			int x = s[i]-'a';
			if (trie[rt][x] == 0)
				trie[rt][x] = ++tot;
			
			rt = trie[rt][x];
			sum[rt]++; 		
		}	
	} 
	int find(char *s,int rt)
	{
		int l = strlen(s);
		for (int i = 0; i < l; i++)
		{
			int x = s[i]-'a';
			if (!trie[rt][x]) return 0;
			rt = trie[rt][x];
		}
		return sum[rt];
	}
}Tr;

int main(int argc,char *argv[])
{
	char ch;
	while(gets(s))
	{
		if (s[0]==NULL)
			break;
		Tr.insert(s,0);
	}
	while(gets(s))
		printf("%d\n",Tr.find(s,0));
	return 0;
}

LUOGU-2580

对字符串查询操作.求询问串作为前缀是否出现,是否第一次出现,是否没出现.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#pragma GCC optmize("0fuck")
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6+10;
char s[10];
char ss[4][10] = {"WRONG","REPEAT","OK"};
struct Trie{
	int tot,trie[maxn][26];
	bool vis[maxn];
	void settledown(void)
	{
		tot = 1;
		memset(vis,1,sizeof(vis));
	}
	void insert(char *s,int rt)
	{
		int l = strlen(s+1);
		for (int i = 1; i <= l; i++)
		{
			int x = s[i]-'a';
			if (trie[rt][x] == 0)
				trie[rt][x] = ++tot;
			rt = trie[rt][x]; 	
		}	
	} 
	int find(char *s,int rt)
	{
		int l = strlen(s+1);
		for (int i = 1; i <= l; i++)
		{
			int x = s[i]-'a';
			if (!trie[rt][x]) return 0;
			rt = trie[rt][x];
		}
		if (vis[rt]) 
		{
			vis[rt] = 0;
			return 2;
		}
		else return 1;
	}
}Tr;

int main(int argc,char *argv[])
{
	Tr.settledown();
	int n,m;
	scanf("%d",&n);	
	while(n--)
	{
		scanf("%s",s+1);
		Tr.insert(s,1);
	}
	scanf("%d",&m);
	
	while(m--)
	{
		scanf("%s",s+1);
		printf("%s\n",ss[Tr.find(s,1)]);
	}
	return 0;
}

Aho-Corasick Automaton

这玩意才是重点

首先我对于AC自动姬的理解就是

一样的对于模式串建立字典树，在树上算fail数组，我们把这两个玩意放到一起.

Trie只能做前缀不能匹配吧,加了KMP不就行了么!

我觉得有张图挺好的。

AC

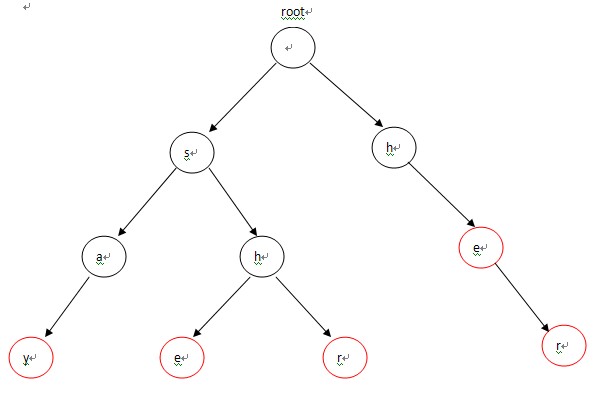
这是普通的建立Trie树的过程

然后我们在上面加上fail数组 / 指针就可以了

AC

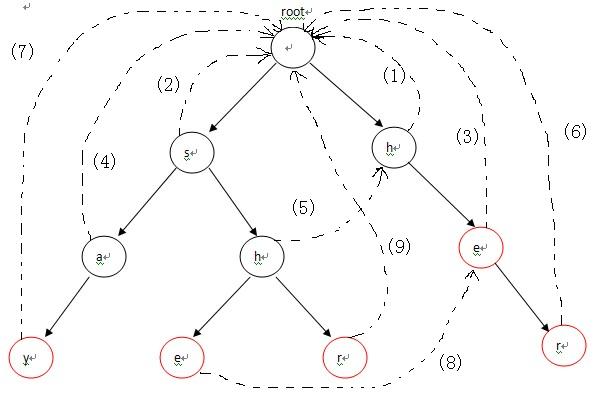
对于AC自动姬,有两种写法

带指针(我还是偏向于喜欢这么写,感觉挺好理解的)

可食用对象

LUOGU-3808

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<bits/stdc++.h>
#include<queue>
using namespace std;
const int maxn = 1e6 + 5;
int cnt,N;
struct node{
    node *next[26];
    node *fail;
    int sum;
};
char key[maxn];
node *newnode,*root;
char pattern[maxn];
void Insert(char *s)
{
    node *p = root;
    for(int i = 0; s[i]; i++)
    {
        int x = s[i] - 'a';
        if(p->next[x] == NULL)
        {
            //newnode=(struct node *)malloc(sizeof(struct node)); 
            newnode = new(node);
            for(int j=0;j<26;j++) newnode->next[j] = 0;
            newnode->sum = 0;newnode->fail = 0;
            p->next[x]=newnode;
        }
        p = p->next[x];
    }
    p->sum++;
}
void build_fail_pointer()
{
    queue<node*>q;
    q.push(root);
    node *p;
    node *temp;
    while(!q.empty())
    {
        temp = q.front();
        q.pop();
        for(int i = 0; i <= 25; i++)
        {
            if(temp->next[i])
            {
                if(temp == root)
                    temp->next[i]->fail = root;
                else
                {
                    p = temp->fail;
                    while(p)
                    {
                        if(p->next[i])
                        {
                            temp->next[i]->fail = p->next[i];
                            break;
                        }
                        p = p->fail;
                    }
                    if(p == NULL) temp->next[i]->fail = root;
                }
                q.push(temp->next[i]);
            }
        }
    }
}
void ac_automation(char *ch)
{
    node *p = root;
    int len = strlen(ch);
    for(int i = 0; i < len; i++)
    {
        int x = ch[i] - 'a';
        while(!p->next[x] && p != root) p = p->fail;
        p = p->next[x];
        if(!p) p = root;
        node *temp = p;
        while(temp != root)
        {
           if(temp->sum >= 0)
           {
               cnt += temp->sum;
               temp->sum = -1;
           }
           else break;
           temp = temp->fail;
        }
    }
}
int main(int argc, char *argv[])
{
	//root=(struct node *)malloc(sizeof(struct node));
    root = new(node); //好像 new(node)更快!? 
    for(int j=0;j<26;j++) root->next[j] = 0;
    root->fail=0;
    root->sum=0;
    scanf("%d",&N);
    getchar();//get char of newline 
    for(int i = 1; i <= N; i++)
    {
        scanf("%s",key);
        Insert(key);
    }
    scanf("%s",pattern);
    cnt = 0;
    build_fail_pointer();
    ac_automation(pattern);
    printf("%d\n",cnt);
    return 0;
}

网上拉来一个不用指针的.

蓝甘冰露

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define il inline
#define RG register
#define N 10010
using namespace std;
 
char s[N][55],ss[N*100];
int n,times[N];//times记录单词在文本串中出现的次数
 
struct Trie{
   int son[N][26],fail[N],root,L,num[N];
   int last[N];//只是一个优化，有没有都没关系
    
   void init(){
      L=1; root=0;
      memset(son,0,sizeof(son));
      memset(num,0,sizeof(num));
      memset(last,0,sizeof(last));
      memset(fail,0,sizeof(fail));
   }
    
   il int idx(char c){ return c-'a'; }
    
   void insert( char s[],int v ){
      int len=strlen(s), cur=root;
      for(int i=0;i<len;i++){
            int id=idx(s[i]);
         if(!son[cur][id])
            son[cur][id]=L++;
         cur=son[cur][id];
      }
      num[cur]=v;   //记录单词编号
   }
    
   void build(){
        int que[N],hd=0,tl=0;
        for(int i=0;i<26;i++)
            if(son[root][i]){
                que[tl++]=son[root][i];
                fail[son[root][i]]=root;
            }
            else son[root][i]=root;
       
        while(hd<tl){
            int cur=que[hd++];
            for(int i=0;i<26;i++){
                int Son=son[cur][i];
                if(Son){
                    int f=fail[cur];
                    while(f && !son[f][i]) f=fail[f];
                    fail[Son]=son[f][i];
                                        num[Son]=num[fail[Son]];//不用last优化时要加上这一句
                                        que[tl++]=Son;
                }
                else son[cur][i]=son[fail[cur]][i];
            }
                        //if( num[fail[cur]] )last[cur]=fail[cur];
                        //else last[cur]=last[fail[cur]];
        }
    }
    
   void query( char s[] ){
        int len=strlen(s),cur=root;
        for(int i=0;i<len;i++){
            int id=idx(s[i]);
            while(cur && !son[cur][id]) cur=fail[cur];
            if(son[cur][id]){
                cur=son[cur][id];
                int k=cur;
                        while(k) times[ num[k] ]++,k=fail[k];
                /*while(k){
                            if(num[k]) times[num[k]]++;
                            k=last[k];
                            }*/
            }
             
        }
    }
    
}AC;
 
int main(){
   scanf("%d",&n); AC.init();
   for(RG int i = 1;i<=n;i++){
      scanf("%s",s[i]);
      AC.insert(s[i],i);
   }
   AC.build();
   scanf("%s",ss); AC.query(ss);
   for( RG int i=1;i<=n;i++ )    printf("%s %d\n",s[i],times[i]);
   return 0;
}