FFT/NTT学习笔记

引言

史诗级巨坑填完再划

主要参考资料：

lych_cys梁大的讲解

MYY的国家集训队论文

Menci’s blog

邓祎明的知乎专栏

学长方尤乐的blog

Miskcoo’s blog

（和一些奇奇怪怪的东西

预备知识

多项式

定义

（参见初中人教版七年级上课本）

系数表示法

将$P(X)=a_0+a_1X+a_2X^2+\cdots+a_nX^n$的每一个$X$ 前的系数$a_i$提取出来看作一个$n+1$维向量

此向量$\vec{a}$就是$P(X)$的系数表示法的向量。

点值表示法

对于这个多项式若我们不知道它的系数,我们可以用采样的方式将一组插值节点$(x_0,x_1,\cdot\cdot\cdot,x_n)$代入上式

得到$n+1$个不同的结果$(y_0,y_1,\cdot\cdot\cdot,y_n)$，就可以唯一确定这个多项式.

点值表示法正确性的证明

• 证明:

  假设原命题不成立即存在两个不同的多项式$A(x),B(x)$在$\forall i\in[0,n]$，都有$A(x_i)=B(x_i)$

  那么假设用$A(x_i)-B(x_i) = H(x_i) = 0$,那么$H(x_i)$有$(n+1)$个根,这与$n$次多项式只有$n$个根的代数基本定理相矛盾，矛盾！故假设不成立！

  $\therefore$原命题正确性显然.

  而$FFT$就是利用了点值和系数表示之间的关系，在快速求点值来表示系数，搭起这两个变换的桥梁.

多项式的乘除法

乘法:叫做卷积,也作奆积。形象地可以写成:

$$c_i=\sum_{j=0}^{i}a_j*b_{i-j}$$

用这个公式不难得到一个$O(n^2)$的算法.

除法:就是大除法,小学/初中奥数部分不赘述了.

单位根及其性质

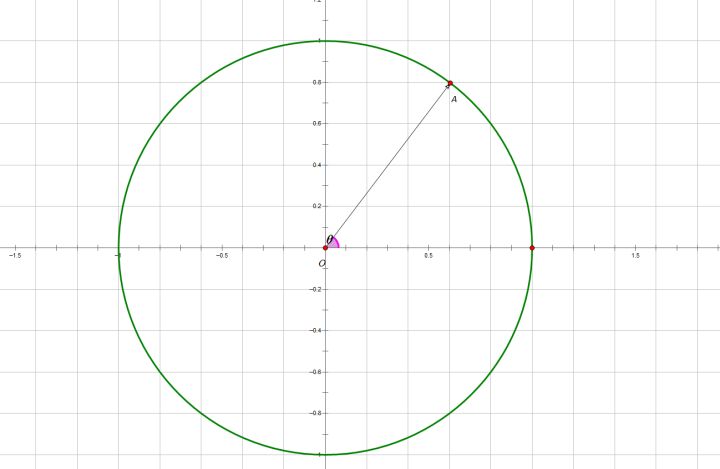
证明一：

由几何意义，这两者表示的向量终点是相反的，左边较右边在单位圆上多转了半圈。

证明二：

由计算的公式：

最后一步由三角恒等变换得到。

FFT(法法塔)

但是这样的操作常数爆炸..FFT本身的常数就很奆..

观察分组情况

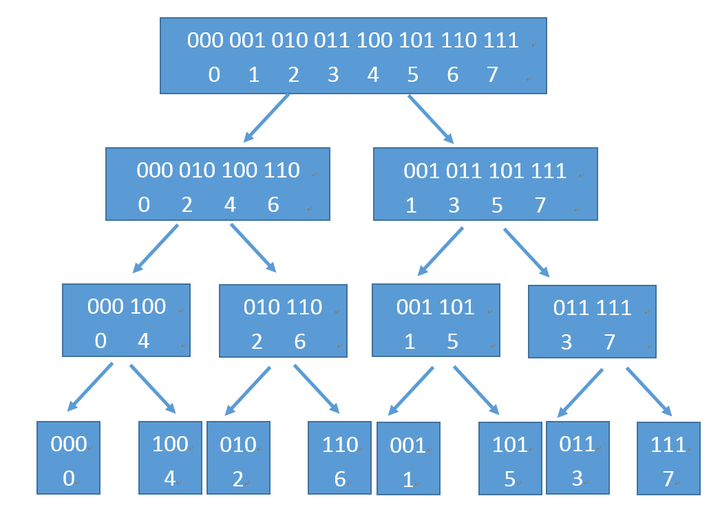
//递归爆栈 LUOGU热掉77分 
#include<bits/stdc++.h>
#define complex COMPLEX
//complex关键字也是服了 
using namespace std;
const int MAXN=2*1e6+10;
inline int read()
{
    char c=getchar();int x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (const complex &a,const complex &b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (const complex &a,const complex &b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (const complex &a,const complex &b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分 
void FFT(int limit,complex *a,int type)
{
    if(limit==1) return ;
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    FFT(limit>>1,a1,type);
    FFT(limit>>1,a2,type);
    complex Wn=complex(cos(2.0*Pi/limit) , type*sin(2.0*Pi/limit)),w=complex(1,0);
    for(int i=0;i<(limit>>1);i++,w=w*Wn)//这里的w相当于公式中的k 
        a[i]=a1[i]+w*a2[i],
        a[i+(limit>>1)]=a1[i]-w*a2[i];//利用单位根的性质，O(1)得到另一部分 
}
int main(int argc, char *argv[])
{
    int N=read(),M=read();
    for(int i=0;i<=N;i++) a[i].x=read();
    for(int i=0;i<=M;i++) b[i].x=read();
    int limit=1;while(limit<=N+M) limit<<=1;
    FFT(limit,a,1);
    FFT(limit,b,1);
    for(int i=0;i<=limit;i++)
        a[i]=a[i]*b[i];
    FFT(limit,a,-1);
    for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/limit+0.5));
	return 0;
}

递归爆栈..没话说了.

改迭代

#include<bits/stdc++.h> 
#define complex COMPLEX
//complex关键字也是服了 
using namespace std;
const int MAXN=1e6+10;
inline int read()
{
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (const complex &a,const complex &b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (const complex &a,const complex &b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (const complex &a,const complex &b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分 
int N,M;
int l,r[MAXN];
int limit=1;
void FFT(complex *A,int type)
{
	for (int i = 0; i < limit; i++)
		if (i < r[i]) swap(A[i],A[r[i]]);
	for (int mid = 1; mid < limit; mid<<=1)
	{
		complex Wn(cos(Pi/mid),type*sin(Pi/mid));
		for (int R = mid<<1,j = 0; j <limit;j+=R)
		{
			complex w(1,0);
			for (int k = 0; k < mid; k++,w=w*Wn)
			{
				complex x=A[j+k],y=w*A[j+mid+k];
				A[j+k] = x+y;
				A[j+mid+k] = x-y;
			}
		}
	}
}
int main(int argc, char *argv[])
{
    int N=read(),M=read();
    for(int i=0;i<=N;i++) a[i].x=read();
    for(int i=0;i<=M;i++) b[i].x=read();
    while(limit<=N+M) limit<<=1,l++;
    for(int i=0;i<limit;i++)
        r[i]= ( r[i>>1]>>1 )| ( (i&1)<<(l-1) ) ;
    FFT(a,1);
    FFT(b,1);
    for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0;i<=N+M;i++)
        printf("%d ",(int)(a[i].x/limit+0.5));
    return 0;
}

所以说算是差不多学会了FFT

上道题目

LUOGU-1919

大整数乘法用FFT来跑

其实就是规定了$x=10$的FFT.

注意前导0的处理,具体实现看代码.

#include<bits/stdc++.h>
#define complex COMPLEX 
using namespace std;
const int MAXN=1e6+10;
inline int read()
{
    char c=getchar();
    while(c<'0'||c>'9'){c=getchar();}
    if(c>='0'&&c<='9')
	return c-'0';
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}
int N,M;
int l,r[MAXN],ans[MAXN];
int limit=1;
void FFT(complex *A,int type)
{
	for (int i = 0; i < limit; i++)
		if (i < r[i]) swap(A[i],A[r[i]]);
	for (int mid = 1; mid < limit; mid<<=1)
	{
		complex Wn(cos(Pi/mid),type*sin(Pi/mid));
		for (int R = mid<<1,j = 0; j <limit;j+=R)
		{
			complex w(1,0);
			for (int k = 0; k < mid; k++,w=w*Wn)
			{
				complex x=A[j+k],y=w*A[j+mid+k];
				A[j+k] = x+y;
				A[j+mid+k] = x-y;
			}
		}
	}
}
int main(int argc, char *argv[])
{
    int N;scanf("%d",&N); 
	int M = N;
    M--,N--;
    for(int i=0;i<=N;i++) a[i].x=read();
    for(int i=0;i<=M;i++) b[i].x=read();
    while(limit<=N+M) limit<<=1,l++;
    for(int i=0;i<limit;i++)
        r[i]= ( r[i>>1]>>1 )| ( (i&1)<<(l-1) ) ;
    FFT(a,1);
    FFT(b,1);
    for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    FFT(a,-1);
	int i;
    for(i=0;i<=N+M;i++)
    ans[i+100] = (int)(a[i].x/limit+0.5);//向右边平移100位来处理前导0 
    for (int j=M+N+100; j>=100; j--)  
    	while(ans[j] >= 10) ans[j-1] += ans[j]/10,ans[j]%=10;
    i = 0;
    while(!ans[i]) i++;
    for (;i<=M+N+100;i++) 
    	printf("%d",ans[i]);
    return 0;
}

NTT

$NTT$就是快速数论变换,是FFT的虚部变成非浮点而改为Mod一个值的应用.

实部是可以不管的.我们的重点是把虚部转化为其他便于计算的东西.

掌握了关于原根的知识后。就可以得到

$$W_n^n \equiv g^{P-1}\mod{1}$$

所以这个形式只能满足一部分形如$2^n*p+1$的质数,这种质数因为满足费马小定理$a^p\equiv{1}\mod{p}$

叫做费马质数。

//只能Mod费马质数的NTT
#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL a[400010],b[400010],c[400010];
int p=1004535809,g=3,n,m,bin[400010]; 
//p = 2^21*479+1 (Fema Prime)
LL pow(LL a,int b,int mod)
{
    LL ans=1;
    while(b)
    {
        if(b&1) ans=ans*a%mod;
        a=a*a%mod;b>>=1;
    }
    return ans;
}
void ntt(LL *a,int n,int op)
{
    for(int i=0;i<n;i++) if(i<bin[i]) swap(a[i],a[bin[i]]);
    for(int i=1;i<n;i<<=1)
    {
        LL wn=pow((LL)g,op==1?(p-1)/(2*i):p-1-(p-1)/(2*i),p),t,w;
        for(int j=0;j<n;j+=i<<1)
        {
            w=1;
            for(int k=0;k<i;k++)
            {
                t=w*a[i+j+k]%p;w=w*wn%p;
                a[i+j+k]=(a[j+k]-t+p)%p;a[j+k]=(a[j+k]+t)%p;
            }
        }
    }
    if(op==-1)
    {
        LL inv=pow(n,p-2,p);
        for(int i=0;i<n;i++) a[i]=a[i]*inv%p;
    }
}
int main(int argc, char *argv[])
{
    scanf("%d %d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lld",&a[i]);
    for(int i=0;i<=m;i++) scanf("%lld",&b[i]);
    m+=n;n=1;while(n<=m) n<<=1;
    for(int i=0;i<n;i++) bin[i]=(bin[i>>1]>>1)|((i&1)*(n>>1));
    ntt(a,n,1);ntt(b,n,1);
    for(int i=0;i<n;i++) c[i]=a[i]*b[i];ntt(c,n,-1);
    for(int i=0;i<=m;i++) printf("%lld ",c[i]);
    return 0;
}

那么如果不是费马质数

取一个任意的数取模

岂不是要$gg$

因为MYY在论文中提出三次求Mod再CRT(China Remainder Theorem)的做法

就被称为MTT了(雾

模板题

MTT,LUOGU-4245

//对于任意Mod的NTT
//用MYY的三模法.
//%%%%% 
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int P=23333333;
const int M[]= {998244353,1004535809,469762049};
const int G[]= {3,3,3};
const ll _M=(ll)M[0]*M[1];

inline ll Pow(ll a,int b,int p) {
	ll ret=1;
	for (; b; b>>=1,a=a*a%p)
		if (b&1)
			ret=ret*a%p;
	return ret;
}
inline ll mul(ll a,ll b,ll p) {
	a%=p;
	b%=p;
	return ((a*b-(ll)((ll)((long double)a/p*b+1e-3)*p))%p+p)%p;
}
const int m1=M[0],m2=M[1],m3=M[2];
const int inv1=Pow(m1%m2,m2-2,m2),inv2=Pow(m2%m1,m1-2,m1),inv12=Pow(_M%m3,m3-2,m3);
inline int CRT(int a1,int a2,int a3) {
	ll A=(mul((ll)a1*m2%_M,inv2,_M)+mul((ll)a2*m1%_M,inv1,_M))%_M;
	ll k=((ll)a3+m3-A%m3)*inv12%m3;
	return (k*(_M%P)+A)%P;
}
const int N=264000;
struct NTT {
	int P,G;
	int num,w[2][N];
	int R[N];
	void Pre(int _P,int _G,int m) {
		num=m;
		P=_P;G=_G;
		int g=Pow(G,(P-1)/num,P);
		w[1][0]=1;
		for (int i=1; i<num; i++) w[1][i]=(ll)w[1][i-1]*g%P;
		w[0][0]=1;
		for (int i=1; i<num; i++) w[0][i]=w[1][num-i];
		int L=0;while (m>>=1) L++;
		for (int i=1; i<=num; i++) R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
	}
	void FFT(int *a,int n,int r) {
		for (int i=0; i<n; i++) if (i<R[i]) swap(a[i],a[R[i]]);
		for (int i=1; i<n; i<<=1)
			for (int j=0; j<n; j+=(i<<1))
				for (int k=0; k<i; k++) {
					int x=a[j+k],y=(ll)a[j+i+k]*w[r][num/(i<<1)*k]%P;
					a[j+k]=(x+y)%P;
					a[j+i+k]=(x+P-y)%P;
				}
		if (!r) for (int i=0,inv=Pow(n,P-2,P); i<n; i++) a[i]=(ll)a[i]*inv%P;
	}
} ntt[3];
int n,m,n1,n2;
int a[3][N];
int A[N],B[N],C[N],D[N];
int main(int argc, char *argv[]) {
	scanf("%d%d%d",&n1,&n2,&P);
	for (int i=0; i<=n1; i++)
		scanf("%d",&A[i]);
	for (int i=0; i<=n2; i++)
		scanf("%d",&B[i]);
	for (m=1; m<=(n1+n2); m<<=1);
	for (int i=0; i<3; i++) ntt[i].Pre(M[i],G[i],m);
	for (int i=0; i<3; i++) {
		memcpy(C,A,sizeof(int)*(m+5));
		memcpy(D,B,sizeof(int)*(m+5));
		ntt[i].FFT(C,m,1);
		ntt[i].FFT(D,m,1);
		for (int j=0; j<m; j++) C[j]=(ll)C[j]*D[j]%ntt[i].P;
		ntt[i].FFT(C,m,0);
		for (int j=0; j<m; j++) a[i][j]=C[j];
	}
	for (int i=0; i<=n1+n2; i++) printf("%d ",CRT(a[0][i],a[1][i],a[2][i]));
	return 0;
}