终于开始磕高级数据结构了
二叉索引树Binary Index Tree(树状数组)
动态的连续和查询问题,有n个元素的数组
设计一个数据结构,支持以下两种操作:
Add(x,d) 让A[x]增加d
Query(L,R) 计算A[L]+..+A[R].
首先介绍一个玩意叫做lowbit(x)
对于正整数x我们定义它的二进制最右边的1的值为lowbit(x)
在讲BIT之前,我们来先了解一个函数:对于任意正整数x,我们定义lowbit(x)为x的二进制中最右边的1所对应的值,比如,5的二进制是101,那么lowbit(5)= 1;4的二进制是100,那么lowbit(4) = 4;这里用到的是按位运算,请读者自己去查阅关于这点的资料。但为什么呢?计算机里面的整数采用补码表示,-x实际上是x在二进制中按位取反,末位+1后的结果,二者按位取“与”之后,前面全部变成0,之后的lowbit保持不变。
简单的两个操作如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
using namespace std;
const int maxn = 500010;
int n,m,a[maxn],C[maxn];
int sum(int x)
{
int ret = 0;
while(x)
{
ret += C[x];
x -= lowbit(x);
}
return ret;
}
void add(int x,int d)
{
while(x <= n)
{
C[x] += d;
x += lowbit(x);
}
}
int query(int l,int r){return (sum(r)-sum(l-1));}
int main(int argc, char *argv[])
{
memset(C,0,sizeof(C));
scanf("%d%d",&n,&m);
for (int i = 1; i <= n; i++)
{
int x;
scanf("%d",&x);
a[i] = x;
add(i,x);
}
while(m--)
{
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",query(x,y));
}
return 0;
}
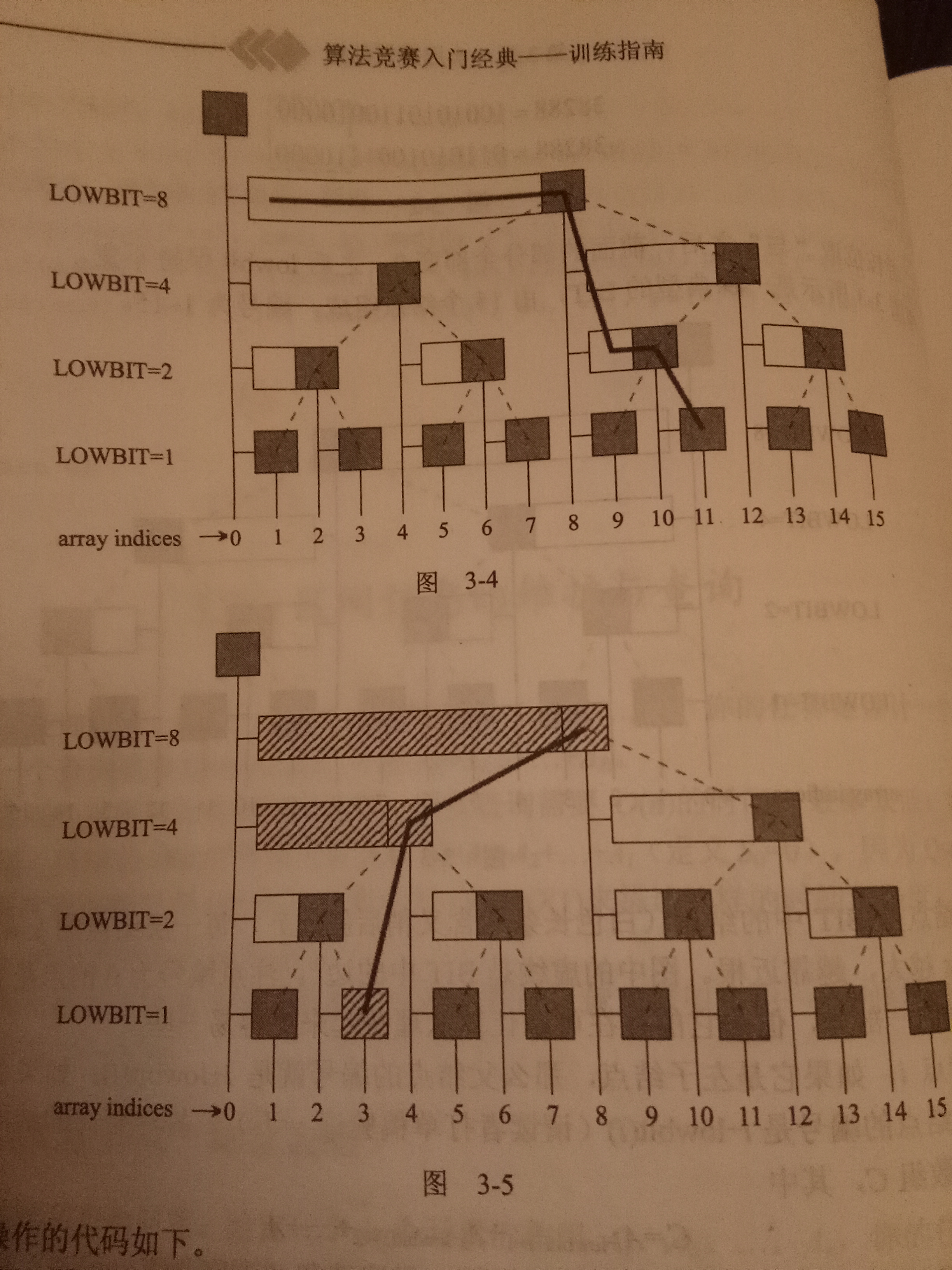
主要是add和sum这两个操作
可以用蓝书上两张图记忆
LA-4329 Ping Pong
传送门:LA-4329
题目大意:
给定一个n个元素的数组,每个元素都有位置和实力两个权值,求三元组(al,ar,ap)的个数,其中要求无论是位置还是实力值都要满足l<p<r.
思路:加法原理,我们只要求出在第i个人当裁判的时候在前后比a[i]小或是比a[i]大的个数,就可以用乘法原理和加法原理计算了。
所以问题转化为求这个比a[i]小的c[i]和比a[i]大的d[i]即可.要求动态,这样就可以套上树状数组了。
代码如下
1 |
|
RMQ问题
RMQ,即Range Minimum Query,要求给出一个n个元素的数值,能够查询出区间范围内的元素最小值
ST(Sparse Table)表
O(nlogn) ~ O(1)
利用递推的思想,令d(i,j)表示从i开始,长度为2^j的一段元素中的最小值,那么有这样的递推式
d(i,j)= min(d(i,j-1),d(i+2^(j-1),j-1));
不难写出这样的代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36//RMQ问题
using namespace std;
const int maxn = 1e4+10;
int a[maxn];
int d[maxn][100]; // d[maxn][maxlog(n)];
void RMQ_init(int a[],int n)
{
for (int i = 1; i <= n; i++)
d[i][0] = a[i];
for (int j = 1; (1<<j) <= n; j++)
for (int i = 0; i + (1<<j) - 1 <= n; i++) //可以从第0位置开始
d[i][j] = min(d[i][j-1],d[i+(1<<(j-1))][j-1]);
}
int RMQ_query(int l,int r)
{
int k = 0;
while((1<<(k+1)) <= r-l+1) k++;
return min(d[l][k],d[r-(1<<k)+1][k]);
}
int main(int argc, char *argv[])
{
int n,t,q,x;
scanf("%d",&n);
for (int i = 1; i <= n; i++)
scanf("%d",&a[i]);
RMQ_init(a,n);
scanf("%d",&q);
while(q--)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",RMQ_query(l,r));
}
return 0;
}
笛卡尔树 + LCA + ±RMQ
O(n) ~ O(1)
这是个巨复杂的方法
很难写对 挂个链接就跑
http://blog.csdn.net/john159151/article/details/19411523
线段树
定义
假设有编号从1到n的n个点,每个点都存了一些信息,用[L,R]表示下标从L到R的这些点。
线段树的用处就是,对编号连续的一些点进行修改或者统计操作,修改和统计的复杂度都是O(log2(n)).
线段树的原理,就是,将[1,n]分解成若干特定的子区间(数量不超过4 * n),然后,将每个区间[L,R]都分解为少量特定的子区间,通过对这些少量子区间的修改或者统计,来实现快速对[L,R]的修改或者统计。
所以满足用线段树解决的题目必须要能够符合区间加法的原则,保证分成的子区间L,R能够得到正确的统计结果,换言之,要能够满足子区间答案之和为总区间答案的原则。
符合区间加法的例子:
数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );
最大值——总最大值=max(左区间最大值,右区间最大值)
不符合区间加法的例子:
众数——只知道左右区间的众数,没法求总区间的众数
01序列的最长连续零——只知道左右区间的最长连续零,没法知道总的最长连续零
原理
线段树本质上是维护下标为1,2,..,n的n个按顺序排列的数的信息,所以,其实是“点树”,是维护n的点的信息. 线段树是将每个区间[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 这里的除法是整数除法,即对结果下取整)直到 L==R 为止。 开始时是区间[1,n] ,通过递归来逐步分解,假设根的高度为1的话,树的最大高度为
线段树对于每个n的分解是唯一的,所以n相同的线段树结构相同,这也是实现可持久化线段树的基础。
关于lazy标记思想:
线段树的区间修改也是将区间分成子区间,但是要加一个标记,称作懒惰标记。
标记的含义:
本节点的统计信息已经根据标记更新过了,但是本节点的子节点仍需要进行更新。即,如果要给一个区间的所有值都加上1,那么,实际上并没有给这个区间的所有值都加上1,而是打个标记,记下来,这个节点所包含的区间需要加1.打上标记后,要根据标记更新本节点的统计信息,比如,如果本节点维护的是区间和,而本节点包含5个数,那么,打上+1的标记之后,要给本节点维护的和+5。这是向下延迟修改,但是向上显示的信息是修改以后的信息,所以查询的时候可以得到正确的结果。有的标记之间会相互影响,所以比较简单的做法是,每递归到一个区间,首先下推标记(若本节点有标记,就下推标记),然后再打上新的标记,这样仍然每个区间操作的复杂度是O(log2(n))。
标记有相对标记和绝对标记之分:
相对标记是将区间的所有数+a之类的操作,标记之间可以共存,跟打标记的顺序无关(跟顺序无关才是重点)。
所以,可以在区间修改的时候不下推标记,留到查询的时候再下推。
注意:如果区间修改时不下推标记,那么PushUp函数中,必须考虑本节点的标记。而如果所有操作都下推标记,那么PushUp函数可以不考虑本节点的标记,因为本节点的标记一定已经被下推了(也就是对本节点无效了)
绝对标记是将区间的所有数变成a之类的操作,打标记的顺序直接影响结果,所以这种标记在区间修改的时候必须下推旧标记,不然会出错。
注意,有多个标记的时候,标记下推的顺序也很重要,错误的下推顺序可能会导致错误。
具体实现
在线段树中 我们可以采用数组构造完全二叉树的方式,使得如果根节点为rt,左儿子就为2 rt,右儿子就为2 rt+1.
但是可以装个bi这么写1
2
单点修改
下面以codevs1080的单点修改求区间和的例子演示具体写法
传送门:Codevs-10801
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
using namespace std;
const int maxn = 1e5+7;
int n,m,a[maxn];
struct SegmentTree{
int sum[maxn<<2],lazy[maxn<<2];
void Pushup(int rt){sum[rt] = sum[lc]+sum[rc];}
void Pushdown(int rt,int ln,int rn)
{
if(lazy[rt])
{
lazy[lc]+=lazy[rt];
lazy[rc]+=lazy[rt];
sum[lc]+=lazy[rt]*ln;
sum[rc]+=lazy[rt]*rn;
lazy[rt] = 0;
}
}
void build(int l,int r,int rt)
{
if (l == r)
{
sum[rt] = a[l];
return ;
}
int mid = (l+r) >> 1;
build(l,mid,lc);
build(mid+1,r,rc);
Pushup(rt);
}
void update(int q,int v,int l,int r,int rt)//A[q] += v;
{
if (l == r)
{
sum[rt] += v;
return ;
}
int mid = (l+r) >> 1;
if (q <= mid) update(q,v,l,mid,lc);
else update(q,v,mid+1,r,rc);
Pushup(rt);
}
int query(int L,int R,int l,int r,int rt)
{
if (L <= l && r <= R) return sum[rt];
int mid = (l+r) >> 1;
Pushdown(rt,mid-l+1,r-mid);
int ans = 0;
if (L <= mid) ans += query(L,R,l,mid,lc);
if (R > mid) ans += query(L,R,mid+1,r,rc);
return ans;
}
}Tree;
int main(int argc, char *argv[])
{
scanf("%d",&n);
for (int i = 1; i <= n; i++)
scanf("%d",&a[i]);
Tree.build(1,n,1);
scanf("%d",&m);
while(m--)
{
int opt,x,y;
scanf("%d%d%d",&opt,&x,&y);
if (opt == 1)
Tree.update(x,y,1,n,1);
else
printf("%d\n",Tree.query(x,y,1,n,1));
}
return 0;
}
一遍就过了真是神奇
区间修改
大致格式差不多长这个样子
1 | void Change(int p, int l, int r, int L, int R) |
这个玩意撸了好久啊。蓝书问题3.2.4(2)
1 |
|
还有一个写法稍微不一样的板子
但是和蓝书上面的两个问题是匹配的
挂上来咯1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
using namespace std;
const int maxn = 100000+ 10;
//update_add:把A[L]~A[R]的值全部加v_add
//update_set:把A[l]~A[R]的值设为v_set
//query:计算子序列的元素和,最小值,最大值
int sumv[2*maxn],minv[2*maxn],maxv[2*maxn];
int addv[2*maxn], setv[2*maxn];
int y11, y2, v_add, v_set;
void maintain(int o, int L, int R) {
int lc = 2*o, rc = 2*o + 1;
sumv[o] = minv[o] = maxv[o] = 0;
if(setv[o] >= 0) {
sumv[o] = setv[o] * (R-L+1);
minv[o] = maxv[o] = setv[o];
}
else if(R > L) {
sumv[o] = sumv[lc] + sumv[rc];
minv[o] = min(minv[lc], minv[rc]);
maxv[o] = max(maxv[lc], maxv[rc]);
}
minv[o] += addv[o]; maxv[o] += addv[o]; sumv[o] += addv[o] * (R-L+1);
}
void pushdown(int o) {
int lc = 2*o, rc = 2*o+1;
if(setv[o] >= 0) {
setv[lc] = setv[rc] = setv[o];
addv[lc] = addv[rc] = 0;
setv[o] = -1;
}
if(addv[o] > 0) {
addv[lc] += addv[o];
addv[rc] += addv[o];
addv[o] = 0;
}
}
void update_add(int o, int L, int R) {
int lc = 2*o, rc = o*2+1;
if(y11 <= L && y2 >= R) {
addv[o] += v_add;
}
else {
pushdown(o);
int M = L + (R-L)/2;
if(y11 <= M) update_add(lc, L, M); else maintain(lc, L, M);
if(y2 > M) update_add(rc, M+1, R);else maintain(rc, M+1, R);
}
maintain(o, L, R);
}
void update_set(int o, int L, int R) {
int lc = 2*o, rc = o*2+1;
if(y11 <= L && y2 >= R) {
setv[o] = v_set;
addv[o] = 0;
}
else {
pushdown(o);
int M = L + (R-L)/2;
if(y11 <= M) update_set(lc, L, M); else maintain(lc, L, M);
if(y2 > M) update_set(rc, M+1, R); else maintain(rc, M+1, R);
}
maintain(o, L, R);
}
int _min, _max, _sum;
void query(int o, int L, int R, int add) {
if(setv[o] >= 0) {
_sum += (add+setv[o]+addv[o]) * (min(R, y2)-max(L, y11)+1);
_min = min(_min, setv[o]+addv[o]+add);
_max = max(_max, setv[o]+addv[o]+add);
}
else if(y11 <= L && y2 >= R) {
_sum += sumv[o] + add * (R-L+1);
_min = min(_min, minv[o]+add);
_max = max(_max, maxv[o]+add);
}
else {
int M = L + (R-L)/2;
if(y11 <= M) query(o*2, L, M, add+addv[o]);
if(y2 > M) query(o*2+1, M+1, R, add + addv[o]);
}
}
void init() {
memset(setv, -1, sizeof setv);
memset(addv, 0, sizeof addv);
memset(sumv, 0, sizeof sumv);
memset(minv, 0, sizeof minv);
memset(maxv, 0, sizeof maxv);
}
int main(int argc, char *argv[])
{
int n,m;
scanf("%d",&n);
for (int i = 1; i <= n; i++)
{
scanf("%d",&v_add);
y11 = y2 = i;
update_add(1,1,n);
}
scanf("%d",&m);
while(m--)
{
int x,a,b,c;
scanf("%d",&x);
if (x == 1)
{
scanf("%d %d %d",&y11,&y2,&c);
v_add = c;
update_add(1,1,n);
}
else
{
_sum = 0;
scanf("%d",&y11);
y2 = y11;
query(1,1,n,0);
printf("%d\n",_sum);
}
}
return 0;
}
划一下习题.
树状数组:
